для чего нужна двоичная система
Двоичная система счисления
Все что-то слышали о двоичной системе счисления, все знают, что это некий «язык компьютеров». Но почему именно так? Почему не пользоваться привычной десятичной системой? В чем, собственно, смысл?
Что такое двоичная система? Это позиционная система счисления с основанием 2. Вот только цифры «два» в ней нет, есть только 0 и 1, и так как цифры две, система называется двоичной (бинарной).
Современный цифровой язык, это ноли и единицы, больше ничего и не нужно. Самое интересное, так называемый машинный код использовался людьми задолго до появления самих машин, а, возможно, даже по появления чисел.
Зачем нужна двоичная система
Двоичная, или бинарная система счисления удобна своей простотой. С помощью комбинации нолей и единиц можно записать любой число и любую букву, что угодно может быть закодировано таким образом.
Но главное, что значения всего два. Это либо «ноль», либо «единица». Сигнал либо есть, либо его нет, свет горит или не горит, есть отверстие или нет (перфокарта), намагничен сектор или размагничен… Аналогии можно приводить бесконечно. Главное, что кодировать сигнал просто. Не нужно создавать сложные механизмы или устройства, достаточно только двух состояний.
Например, еще до того как люди научились считать и писать, сигналы передавались с помощью дыма от костра или ударов в барабаны.
Бинарная система — это просто, ничего проще просто нет. Есть, конечно, и древнейшая унитарная система, где значение всего одно (например, только 1) но с ее помощью нельзя ничего закодировать.
В любой микросхеме транзистор может прибывать в двух положениях «закрыто» или «открыто» (0 или 1) ток пропускается или нет.
Кстати, азбука Морзе — это тоже двоичный код (точка или тире), так же, как и древнейшая сигнальная система — «оптический телеграф». Это это просто огонь костра, который можно закрыть и открыть (огонь есть, или огня нет) ночью, а днем так же использовать дым.
Да, двоичная система используется потому, что с ее помощью удобно кодировать информацию, нужны всего 2 значения. Но удобно ли это считать?
Как считать
Как использовать двоичную систему для записи чисел? Так же как и десятичную. Самым простым примером можно считать кодовый замок, такой как на чемоданах. Каждый диск которого, вращается и может принимать значение от 0 до 9. Достаточно представить, что вместо десяти цифр есть только 2, ноль и единица.
Так как система позиционная, это будет выглядит так:
Сейчас здесь записано число «ноль». Чтобы получилась единица, нужно провернуть крайний правый диск один раз.
Начинается самое интересное, как будет выглядеть число «два»? Крутим правое колесико… И снова получаем 0, ведь других значений нет. Нужно поступить так же, как и в десятичной системе, перенести разряд влево. Только в десятичной, это происходит когда значение превышает 9, а в двоичной сразу после 1.
| Двоичная система | Десятичная система |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Сто в двоичной системе — это 1100100.
Очень интересно в бинарной системе выглядит таблица умножения:
Легко запомнить, неправда ли? 0*0=0, 0*1=0, 1*1=1… И все!
Все математические операции выполняются точно так же
Если сложит в столбик то получается нагляднее
100
Складываем ноли, получаем 0, складываем две единицы, получаем ноль (2 раза провернули диск) и единичку переносим вправо.
Как видите, математика та же, вот только запись чисел неудобная, слишком много нолей и единиц, для человека — неудобно, машине же все равно.
Так же как с цифрами можно поступить с буквами. Латинская буква «a» будет выглядеть как 01001010 кириллическая «а» — 000011100010111000011001, и даже пробел — 00010100.
История создания
Ясно, что человечество пользовалось двоичным кодом очень давно. И сигнальные системы с дымом от костров и даже китайская Книга Перемен (700 лет до нашей эры) с ее гексаграммами известны очень давно. Но окончательно практический смысл бинарный код получил совсем недавно (если не считать азбуку Морзе).
Великий Лейбниц занимался двоичной системой в 17 веке, но применить бинарную систему счисления было особо негде. В том же Веке Паскаль создал свою счетную машину (суммирующую), использующую десятичную систему. Оказалось, что считать на таком «калькуляторе» не так уж и удобно.
Суммирующая машина Паскаля (десятичная)
И только в 40-х годах 20 веке, вместе с появлением первых электронный вычислительных машин двоичный код явил всю свою безусловную полезность и красоту. Именно как машинный язык. Записывать информацию в котором гораздо проще, чем привычными нам средствами, буквами и цифрами.
То же самое, в двоичном коде можно сделать проще
Для чего нужна двоичная система счисления сегодня, мы прекрасно знаем, у каждого в кармане есть смартфон. На самом деле, ноли и единицы используются намного чаще, чем десятичная система, даже если мы, люди, этого и не видим. Не удивительно, мы использовали двоичную систему на протяжении всей истории, но до эры машин даже не замечали этого.
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Большое спасибо! Очень хорошо объяснили. Всё понял.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
поделитесь, пожалуйста, еще постами по информатике если есть
А теперь слушайте домашнее задание: построить синхрофазотрон.
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
На самом деле все еще проще.
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
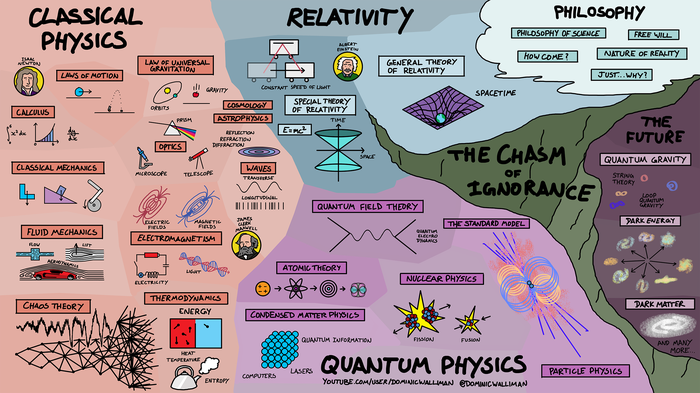
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.
Двоичное счисление на пальцах
Все знают, что компьютеры состоят из единиц и нулей. Но что это значит на самом деле?
Если у вас в школе была информатика, не исключено, что там было упражнение на перевод обычных чисел в двоичную систему и обратно. Маловероятно, что кто-то вам объяснял практический смысл этой процедуры и откуда вообще берётся двоичное счисление. Давайте закроем этот разрыв.
Эта статья не имеет практической ценности — читайте её просто ради интереса к окружающему миру. Если нужны практические статьи, заходите в наш раздел «Где-то баг», там каждая статья — это практически применимый проект.
Отличный план
Чтобы объяснить всё это, нам понадобится несколько тезисов:
Система записи — это шифр
Если у нас есть девять коров, мы можем записать их как 🐄🐄🐄🐄🐄🐄🐄🐄🐄 или как 9 × 🐄.
Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.
Допустим, к нашему стаду прибиваются еще 🐄🐄🐄. Теперь у нас 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄 — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.
Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × 🐄 — это не то же самое, что 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄. Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.
Мы привыкли шифровать десятью знаками
У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.
Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.
Например, перед нами число 19 547. Мы знаем, что в нём есть:
Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:
Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.
Система записи — это условность
Представим бредовую ситуацию: у нас не 10 пальцев, а 6. И в школе нас учили считать не десятками, а шестёрками. И вместо привычных цифр мы бы использовали знаки ØABCDE. Ø — это по-нашему ноль, A — 1, B — 2, E — 5.
Вот как выглядели бы привычные нам цифры в этой бредовой системе счисления:
| 0 — Ø 1 — A 2 — B 3 — C 4 — D 5 — E | 6 — AØ 7 — AA 8 — AB 9 — AC 10 — AD 11 — AE | 12 — BØ 13 — BA 14 — BB 15 — BC 16 — BD 17 — BE | 18 — CØ 19 — CA 20 — CB 21 — CC 22 — CD 23 — CE | 24 — DØ 25 — DA 26 — DB 27 — DC 28 — DD 29 — DE | 30 — EØ 31 — EA 32 — EB 33 — EC 34 — ED 35 — EE | 36 — AØØ 37 — AØA 38 — AØB 39 — AØC 40 — AØD 41 — AØE |
В этой системе мы считаем степенями шестёрки. Число ABADØ можно было бы перевести в привычную нам десятичную запись вот так:
A × 6 4 = 1 × 1296 = 1296
B × 6 3 = 2 × 216 = 432
1296 + 432 + 36 + 24 + 0 = 1788. В нашей десятичной системе это 1788, а у людей из параллельной вселенной это ABADØ, и это равноценно.
Выглядит бредово, но попробуйте вообразить, что у нас в сумме всего шесть пальцев. Каждый столбик — как раз шесть чисел. Очень легко считать в уме. Если бы нас с детства учили считать шестёрками, мы бы спокойно выучили этот способ и без проблем всё считали. А счёт десятками вызывал бы у нас искреннее недоумение: «Что за бред, считать числом AD? Гораздо удобнее считать от Ø до E!»
То, как мы шифруем и записываем числа, — это следствие многовековой традиции и физиологии. Вселенной, космосу, природе и стадам коров глубоко безразлично, что мы считаем степенями десятки. Природа не укладывается в эту нашу систему счёта.
Двоичная система (тоже нормальная)
Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.
Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:
9 — 💡 ⚫⚫ 💡
10 — 💡 ⚫ 💡 ⚫
11 — 💡 ⚫ 💡 💡
12 — 💡 💡 ⚫⚫
13 — 💡 💡 ⚫ 💡
14 — 💡 💡 💡 ⚫
15 — 💡 💡 💡 💡
17 — 💡 ⚫⚫⚫ 💡
18 — 💡 ⚫⚫ 💡 ⚫
19 — 💡 ⚫⚫ 💡 💡
20 — 💡 ⚫ 💡 ⚫⚫
21 — 💡 ⚫ 💡 ⚫ 💡
21 — 💡 ⚫ 💡 💡 ⚫
23 — 💡 ⚫ 💡 💡 💡
24 — 💡 💡 ⚫⚫⚫
25 — 💡 💡 ⚫⚫ 💡
26 — 💡 💡 ⚫ 💡 ⚫
27 — 💡 💡 ⚫ 💡 💡
28 — 💡 💡 💡 ⚫⚫
29 — 💡 💡 💡 ⚫ 💡
30 — 💡 💡 💡 💡 ⚫
31 — 💡 💡 💡 💡 💡
33 — 💡 ⚫⚫⚫⚫ 💡
34 — 💡 ⚫⚫⚫ 💡 ⚫
35 — 💡 ⚫⚫⚫ 💡 💡
36 — 💡 ⚫⚫ 💡 ⚫⚫
37 — 💡 ⚫⚫ 💡 ⚫ 💡
38 — 💡 ⚫⚫ 💡 💡 ⚫
39 — 💡 ⚫⚫ 💡 💡 💡
40 — 💡 ⚫ 💡 ⚫⚫⚫
41 — 💡 ⚫ 💡 ⚫⚫ 💡
42 — 💡 ⚫ 💡 ⚫ 💡 ⚫
43 — 💡 ⚫ 💡 ⚫ 💡 💡
44 — 💡 ⚫ 💡 💡 ⚫⚫
45 — 💡⚫💡💡⚫💡
46 — 💡⚫💡💡💡⚫
47 — 💡⚫💡💡💡💡
48 — 💡💡⚫⚫⚫⚫
49 — 💡💡⚫⚫⚫💡
50 — 💡💡⚫⚫💡⚫
51 — 💡💡⚫⚫💡💡
52 — 💡💡⚫💡⚫⚫
53 — 💡💡⚫💡⚫💡
54 — 💡💡⚫💡💡⚫
55 — 💡💡⚫💡💡💡
56 — 💡💡💡⚫⚫⚫
57 — 💡💡💡⚫⚫💡
58 — 💡💡💡⚫💡⚫
59 — 💡💡💡⚫💡💡
60 — 💡💡💡💡⚫⚫
61 — 💡💡💡💡⚫💡
62 — 💡💡💡💡💡⚫
63 — 💡💡💡💡💡💡
Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:
256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332
Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.
Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.
Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)
Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.
Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить 💡⚫⚫ и ⚫⚫💡, получится 💡⚫💡. Мы писали об этом подробнее в статье о сложении через транзисторы.
Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.
И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.
При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.
Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.