для чего нужна теория вероятности
Для чего нужна теория вероятностей
Особенно широко теория вероятностей применяется для исследования природных явлений. Все протекающие в природе процессы, все физические явления в той или иной степени не обходятся без присутствия элемента случайности. Как бы точно не был поставлен опыт, как бы точно ни были бы зафиксированы результаты эмпирических исследований при повторном проведении эксперимента, результаты будут отличаться от вторичных данных.
При решении многих задач их исход зависит от большого количества факторов, которые сложно зарегистрировать или учесть, но они оказывают огромное значение на конечный результат. Порой количество этих второстепенных факторов так много, и они оказывают настолько большое влияние, что учесть их классическими методами просто невозможно. Так, например, это задачи на определение движения планет Солнечной системы, прогнозы погоды, длина прыжка спортсмена, вероятность встречи знакомого по пути на службу и различные ситуации на фондовой бирже.
Теория вероятностей применима в робототехнике. Например, некое автоматизированное устройство (первичная заготовка робота) выполняет определенные вычисления. В то время как она ведет расчеты, снаружи на нее систематически воздействуют различными помехами, незначительными для системы, но сказывающимися на результатах работы. Задача инженера состоит в том, чтобы определить, с какой частотой будет возникать ошибка, навязанная внешними помехами. Так же методами теории вероятности возможно разработать алгоритм для сведения погрешности вычисления к минимуму.
Задачи подобного рода очень часто встречаются в физике и при разработке новых видов техники. Они требуют тщательного изучения не только главных закономерностей объясняющих основные черты данных явлений в общих их понятиях, но и анализа случайных искажений и возмущений, связанных с действием второстепенных факторов, которые придают исходу опыта в заданных условиях тот самый элемент случайности (неопределенности).
Зачем нужна теория вероятностей в жизни
Именно под таким названием мы и провели вебинар — «Зачем нужна теория вероятностей в жизни».
В вебинаре мы не касались «жёлтых» тем типа «как выигрывать у казино» и «100% способ получить миллион без регистрации и SMS«.
Наоборот, были затронуты более серьёзные. Вот сам вебинар:
Идея похожего математического аппарата используется в Индии: можно купить билетик у мафии и кататься в общественном транспорте бесплатно, а полученные вами штрафы оплатит мафия. Называется «хафта» и выгодно вам и мафии, но не государству.
Подробно разбирается механизм лотереи — как идёт распределение средств и как происходит игра на эмоциях, когда одного победителя показывают по телевизору, а миллионы проигравших — нет. Эта идея была почерпнута из выступления на TED об ошибочных ожиданиях.
Также описывается открытие закона больших чисел и его применение сейчас.
А глядя на карту преступности страны, можно легко увидеть, что в одних регионах в 3 раза меньше шансов стать жертвой преступления, чем в других. Сам термин «уровень преступности» — статистический, это количественная характеристика преступности, и стоит отметить, что когда такой подход к оценке преступности был впервые представлен в 1832 во Франции, он вызвал смятение из-за стабильности полученных данных.
Ещё темы, затронутые в вебинаре:
Кстати, в анонсе вебинара использовался такой факт: в мае 2015 года Россия потеряла управление над космическим аппаратом «Прогресс». Как рассчитать, упадёт ли аппарат на сушу (или на конкретную страну). Сможете дать ответ? На наш взгляд, это отличный пример для иллюстрации геометрического подхода для расчёта вероятностей.
Теория вероятности в жизни людей
Основы теории вероятностей нужно знать каждому человеку для формирования правильного мировоззрения, для осознания того, что мы живем в случайном, вероятностном мире.
Психология человека такова, что ему неуютно среди случайностей. Он жаждет определенности и справедливости, ищет причин и объяснений. Часто таким образом возникают суеверия: например, среди африканских племен распространено поверье о том, что бывают просто львы и львы, в которых переселились души умерших. Последние на людей не нападают. Это объяснение не несет полезной информации, поскольку нет признаков, по которым заранее можно было бы определить, из какой категории лев, но оно успокаивает психологически. Точно так же появляются известные всем суеверия при сдаче экзаменов. Некоторые суеверия, кстати, основаны на частотных совпадениях (например, мелких неприятностей и встреч с черной кошкой). Это относится и к приметам, которые порой подмечают вероятностные закономерности. Так, поговоркам «Беда никогда не приходит одна» или «Жизнь, она полосатая» соответствует в теории вероятностей закон серий.
Следует помнить и то, что мы живем в мире, где происходят случайные события, и то, что закономерности пробиваются через массу случайностей. Чем сложнее система, тем труднее обнаружить закономерности. Именно в этих случаях и используют вероятностные методы. [4]
Таким образом, теория вероятности актуальна в наши дни как в математике и точных науках, так и в нашей повседневной жизни.
Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира [1].
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений, наблюдаемых при многократном повторении опыта [2, с.13].
Теория вероятностей – это раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними [3].
Основные объекты теории вероятностей – случайные события, случайные величины, случайные процессы, то есть фактически весь окружающий нас мир [4, с.6].
Событие – это то, что может произойти или нет при выполнении определённого комплекса условий, или, как говорят, при проведении испытания. Среди возможных событий выделяют достоверные и невозможные. Если при каждом испытании всегда происходит некоторое событие, то оно называется достоверным. Если при испытании некоторое событие заведомо не может произойти, то оно называется невозможным. Если событие не является достоверным или невозможным, то оно часто называется случайным [5, с.10].
Во многих областях человеческой деятельности существуют ситуации, когда определённые явления могут повторяться неограниченное число раз в одинаковых условиях. Анализируя последовательно результаты таких простейших явлений, как подбрасывание монеты, игральной кости, выброс карты из колоды и т.п., мы замечаем две особенности, присущие такого рода экспериментам. Во-первых, не представляется возможным предсказать исход последующего эксперимента по результатам предыдущих, как бы ни было велико число проведённых испытаний. Во-вторых, относительная частота определённых исходов по мере роста числа испытаний стабилизируется, приближаясь к определённому пределу [6, с.8].
Рассмотрим теорию вероятностей на очень простых примерах. Если у нас в ящике лежит 10 пронумерованных шаров с цифрами от 1 до 10, то вероятность вытянуть шар с числом 10 равна 10 процентам. Но более вероятней, что мы вытянем любое другое число от 1 до 9, а не самое большое (не 10), поскольку такая вероятность составляет 90 процентов. Вытянуть шар с самым большим числом из 10000 пронумерованных шаров уже слишком маловероятно. Скорее всего, мы вытянем любое другое число (не 10000). При 10 миллионах шарах вытянуть самое большое число (10000000) практически невозможно [7].
Главным понятием теории вероятностей является вероятность. Это слово «вероятность», синонимом которого является, например, слово «шанс» достаточно часто применяется в повседневной жизни. Думаю, каждому знакомы фразы: «Завтра, вероятно, выпадет снег», или «вероятнее всего в выходные я поеду на природу», или «это просто невероятно», или «есть шанс получить зачет автоматом». Такого рода фразы на интуитивном уровне оценивают вероятность того, что произойдет некоторое случайное событие. В свою очередь математическая вероятность дает некоторую числовую оценку вероятности того, что произойдет некоторое случайное событие.
Теория вероятностей оформилась в самостоятельную науку относительно не давно, хотя история теории вероятностей началась еще в античности. Так, Лукреций, Демокрит, Кар и еще некоторые ученые древней Греции в своих рассуждениях говорили о равновероятностных исходах такого события, как возможность того, что вся материя состоит из молекул. Таким образом, понятие вероятности использовалось на интуитивном уровне, но оно не было выделено в новую категорию. Тем не менее, античные ученые заложили прекрасный фундамент для возникновения этого научного понятия. В средние века, можно сказать, и зародилась теория вероятности, когда были приняты первые попытки математического анализа, таких азартных игр как кости, орлянка, рулетка [8].
Первые подходы к оценке вероятности того или иного события были популярны еще в Средневековье среди «гамлеров» того времени. Однако тогда они имели лишь эмпирическое исследование (то есть оценка на практике, методом эксперимента) [9].
Первые научные работы по теории вероятностей появились в 17 веке. Когда такие ученые как Блез Паскаль и Пьер Ферма открыли некоторые закономерности, которые возникают при бросании костей. В ту же пору к данному вопросу проявлял интерес еще один ученый Христиан Гюйгенс. Он в 1657 в своей работе ввел следующие понятия теории вероятностей: понятие вероятности как величины шанса или возможности; математическое ожидание для дискретных случаев, в виде цены шанса, а также теоремы сложения и умножения вероятностей, которые правда не были сформулированы в явном виде. Тогда же теория вероятностей стала находить сферы своего применения – демографию, страховое дело, оценку ошибок наблюдений [8].
Вероятностные представления довольно успешно применялись ещё в 18 веке такими выдающимися учеными как Лаплас, Лагранж, Лежандр, Гаусс для оценки ошибок измерений, в результате чего уже в то время были заложены основы теории ошибок [10, с.3].
Дальнейшее развитие теории вероятностей привело к необходимости аксиоматизации теории вероятностей и главного понятия – вероятности. Так становление аксиоматики теории вероятностей произошло в 30 гг 20 века. Самый существенный вклад в заложение основ теории внес Космогоров А.Н.
На сегодняшний день теории вероятностей это самостоятельная наука, имеющая огромную сферу применения [8].
Последние десятилетия характеризуются резким повышением интереса к тем разделам математики и ее приложений, которые анализируют явления, носящие «случайный» характер. Эта тенденция в значительной степени объясняется тем, что большинство возникших в последние десятилетия новых математических дисциплин, которое ныне обозначается собирательным термином «кибернетика», оказалось тесно связанным с теорией вероятностей. Тем самым теория вероятностей стала чуть ли не самой первой по прикладному значению из всех математических дисциплин. При этом возникновение новых, в большинстве своем «порожденных» теорией вероятностей наук, скажем «теория игр», «теория информации», «страховая математика» или «стохастическая финансовая математика» привело к положению, при котором теорию вероятностей также приходится рассматривать как объединение большого числа разнородных и достаточно глубоко развитых математических дисциплин [10, с.4].
Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать, или спланировать. В разное время разными способами. В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Споры на эту тему не утихают в самых разных областях науки. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [8]
Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Выпуская на рынок определенный товар, грамотный предприниматель наверняка учтет риски, а также вероятности покупки в том или рынке, стране и т.д. Практически не представляют свою жизнь без теории вероятности брокеры на мировых рынках. Предсказывание денежного курса (в котором точно не обойтись без теории вероятности) на денежных опционах дает возможность зарабатывать на данной теории серьезные деньги.
Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. [9]
Решения чаще всего принимаются эмоционально. Люди боятся летать самолетами. А между тем, самое опасное в полете на самолете – это дорога в аэропорт на автомобиле. Но попробуй кому-то объяснить, что машина опасней самолета. Вероятность того, что пассажир, севший в самолет, погибнет в авиакатастрофе составляет примерно 1/8000000. Если пассажир будет садиться каждый день на случайный рейс, ему понадобится 21000 лет чтобы погибнуть. По исследованиям: в США в первые 3 месяца после терактов 11 сентября 2001 года погибло еще одна тысяча людей. косвенно. Они в страхе перестали летать самолетами и начали передвигаться по стране на автомобилях. А так как это опасней, то количество смертей возросло. По телевидению пугают: птичьим и свиными гриппами, терроризмом, но вероятность этих событий ничтожна по сравнению с настоящими угрозами. Опасней переходить дорогу по зебре, чем лететь на самолете.
Или другой пример – от падения кокосов погибает около 150 человек в год. Это в десятки раз больше, чем от укуса акул. Но фильма «Кокос-убийца» пока не снято. Подсчитано, что шанс человека быть подвергнутым нападению акулы составляет 1 к 11,5 млн, а шанс погибнуть от такого нападения 1 к 264,1 млн. Среднегодовое количество утонувших в США составляет 3306 человек, а погибших от акул 1. Миром правит вероятность и нужно помнить об этом. Они помогут вам взглянуть на мир с точки зрения случая [8].
Таким образом, теорию вероятностей нельзя не применять в нашей жизни. Она имеет разные области применения такие как: биологические и химические процессы, история, экономика, кораблестроение и машиностроение, медицина и большинство различной деятельности человека. Люди применяют её как сознательно, так и подсознательно, что проявляется в обычных повседневных фразах и действиях. Разумный человек должен стремиться мыслить, исходя из законов вероятностей. Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас.
Список использованных источников
Савельева Р. Ю. Основы теории вероятностей и математической статистики [Электронный ресурс]. – Режим доступа: http://открытыйурок.рф/статьи/526665/ (дата обращения – 24.01.2018)
Кибзун А. И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами [Текст]: учебное пособие/А. И. Кибзун, Е. Р. Горяинова, А. В. Наумов, А. Н. Сиротин. – Москва: ФИЗМАТЛИТ, 2002. – 224 с.
Теория вероятностей и основные понятия теории [Электронный ресурс]. – Режим доступа: https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/ (дата обращения 24.01.2018)
Крупкина Т. В. Теория вероятностей и математическая статистика [Текст]: учебное пособие/Т. В. Крупкина, С. В. Бабенышев, Е. С. Кирик. – Красноярск: Сибирский федеральный университет, 2007. – 199 с.
Семенов В. А. Теория вероятностей и математическая статистика [Текст]: учебное пособие/В. А. Семенов. – Санкт-Петербург: Питер, 2013. – 192 с.
Володин И. Н. Лекции по теории вероятностей и математической статистике [Текст]: учебник/И. Н. Володин. – Казань: (Издательство), 2006. – 271 с.
Вишня Ю. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder.com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018)
Агеев В. В. Введение в теорию вероятностей [Текст]: учебно-методическое пособие/В. В. Агеев, М. С. Тихов. – Нижний-Новгород: ФГБОУВПО Нижегородский Государственный университет им. Н.И. Лобачевского Национальный исследовательский университет, 2012. – 32 с.
🎲 Зачем в науке о данных нужны теория вероятностей и статистика
Ilya Ginsburg
С одной стороны, роль теории вероятностей и статистики в машинном обучении сравнительно невелика: используются лишь базовые понятия, хотя и довольно широко. С другой стороны, разведочный анализ данных, их очистка, подготовка и конструирование новых признаков – это чистая статистика. А поскольку эти операции в прикладной науке о данных (Data Science) занимают 90-95% времени, самый важный раздел математики для Data Scientist’ов – именно статистика. Кстати, это отлично демонстрирует разницу между машинным обучением и наукой о данных.
«Вероятности» классификации
Практически все модели классификации, используемые в машинном обучении, на самом деле выдают не единственную метку класса (или его номер), а набор «вероятностей» принадлежности к каждому классу. Логистическая регрессия с бинарной классификацией – это та же линейная регрессия, результат которой пропускается через функцию сигмоиды, преобразующую весь диапазон действительных чисел к диапазону [0,1].
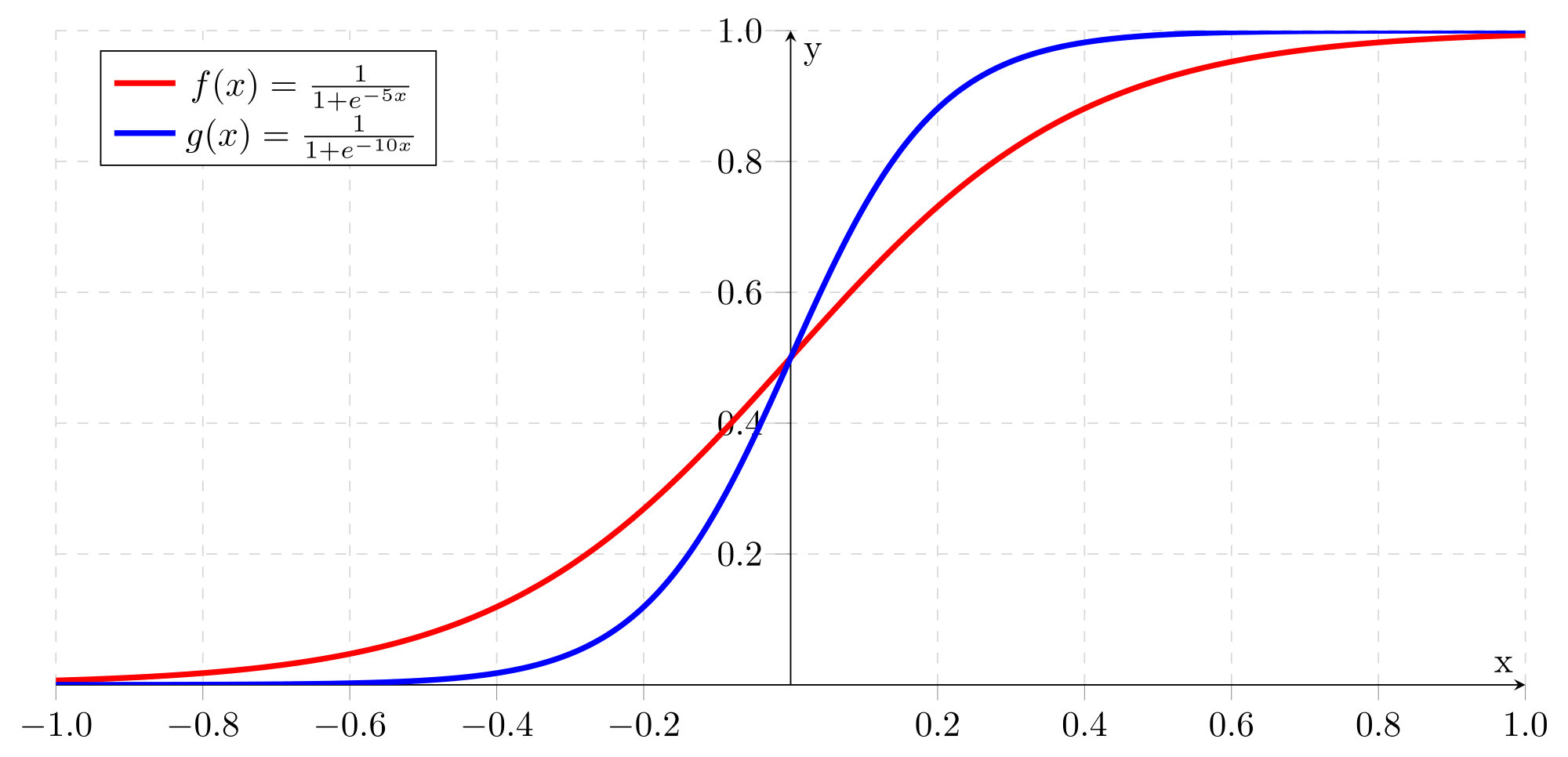
Число p, являющееся результатом сигмоиды, считается «вероятностью» принадлежности результата к одному из классов, а «вероятность» принадлежности к другому классу равна 1-p. Разумеется, это не настоящие вероятности – строго говоря, в данном случае вообще нет смысла говорить о вероятности, ведь результат классификации однозначен. Возможно, в данном случае было бы правильнее называть результат степенью уверенности: например, модель считает, что данный экземпляр принадлежит к классу 1 с уверенностью 74%. Тем не менее, принято называть этот показатель именно вероятностью.
Если классов больше двух, вместо сигмоиды используется Softmax – функция, преобразующая вектор вещественных чисел z размерности N в вектор неотрицательных чисел той же размерности, сумма которых равна 1 (sigma):
В результате мы получаем «вероятности» принадлежности к каждому классу, которые можно интерпретировать по-разному. Традиционно результатом классификации считается класс с максимальной «вероятностью», но ничто не мешает принять какие-то особые меры в тех случаях, когда модель «не уверена» в результате – например, если разница между двумя максимальными «вероятностями» невелика.
Если для классификации используется нейронная сеть, и классов больше двух, последним слоем этой сети практически всегда будет слой Softmax.
Все будет нормально
Нормальное распределение, или распределение Гаусса – это семейство функций плотности распределения вероятности с двумя параметрами: mu (среднее значение, оно же медиана и мода) и sigma (стандартное или среднеквадратическое отклонение). Иногда вместо sigma используется параметр sigma 2 – дисперсия нормального распределения:
График функции плотности нормального распределения похож на колокол. Его центральная координата равна mu, а стандартное отклонение sigma определяет уровень «крутизны» графика: чем оно меньше, чем большая доля значений переменной будет находиться недалеко от центра.
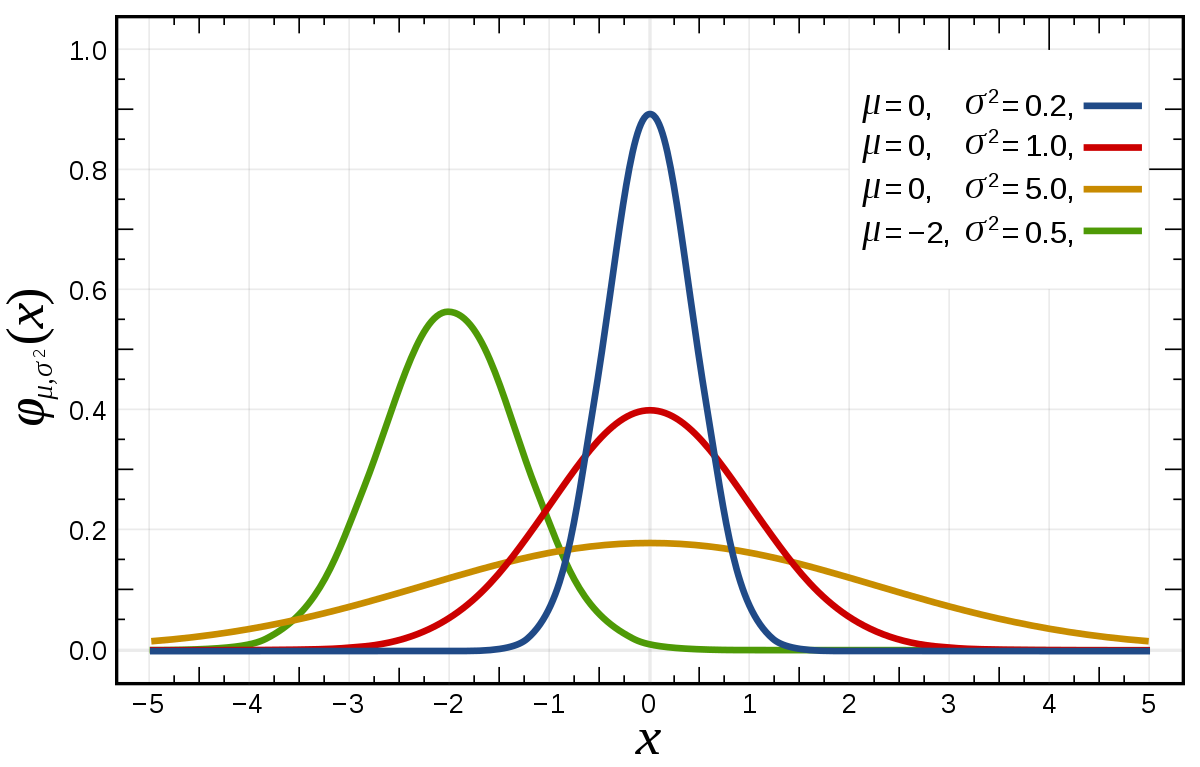
Центральная предельная теорема гласит, что сумма многих слабо зависимых друг от друга случайных величин имеет нормальное распределение – именно поэтому оно имеет огромное значение для статистики, которая обычно анализирует массовые явления. Например, если каждый человек, проходящий мимо кофейни, заходит выпить кофе с определенной вероятностью – то количество посетителей кафе будет иметь нормальное распределение.
Нормальное распределение настолько важно, что многие методы машинного обучения работают намного лучше, если данные нормально распределены (или даже вообще не работают в противном случае). Поэтому нормализация данных – очень часто выполняемая операция, а для нейронных сетей даже разработан слой пакетной нормализации (batch normalization).
Байесовские модели
Разведочный анализ данных
Разведочный анализ данных (exploratory data analysis, EDA) – это изучение данных для принятия решений по поводу их применения, очистки, преобразования и конструирования новых признаков. Как сказано выше, EDA – это чистая статистика, и основные цели его первого этапа – понять вид распределения признаков, основные параметры этого распределения, обнаружить выбросы и т.д.
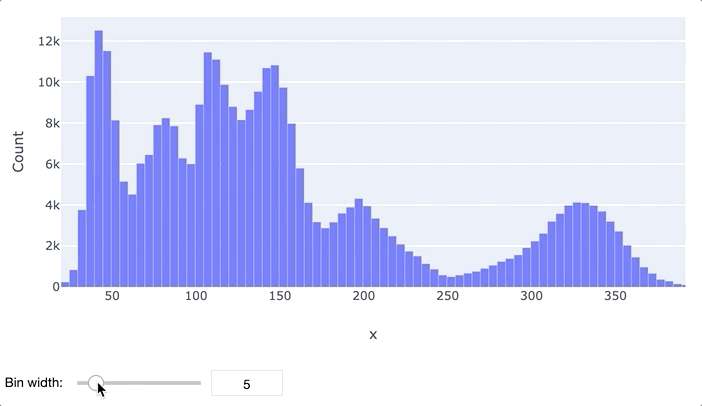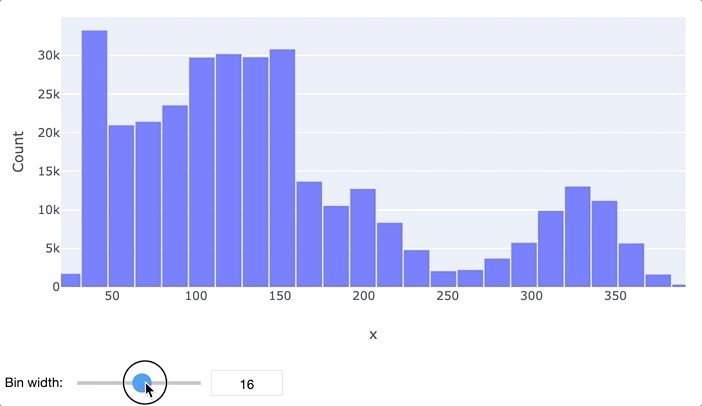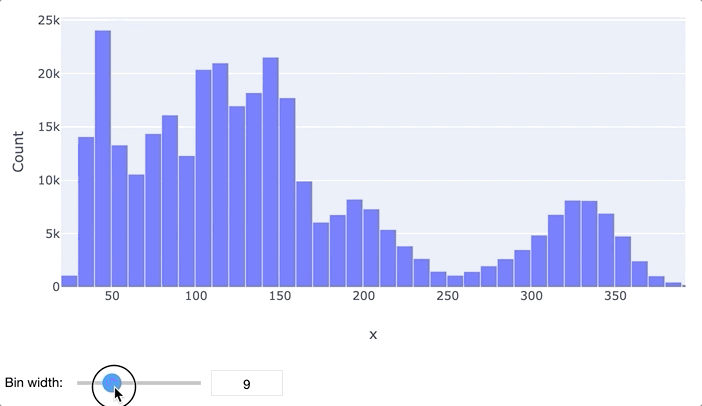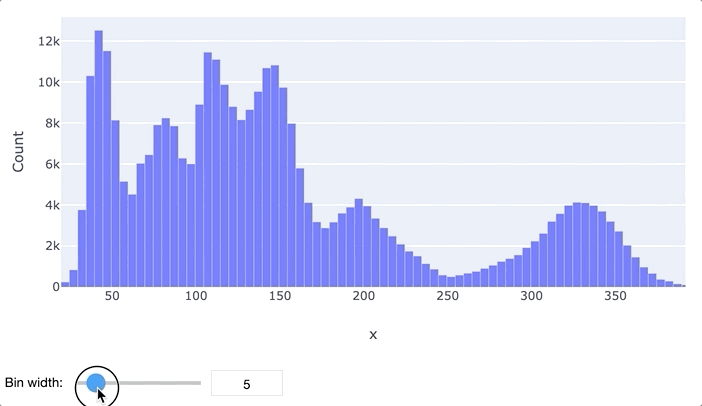
В первую очередь для анализа данных обычно применяются гистограммы и «ящики с усами». Гистограмма просто разбивает весь диапазон данных на несколько отрезков, и для каждого отрезка выводит количество элементов набора данных, попадающих в этот отрезок. Легко заметить, что гистограмма отдаленно похожа на график функции плотности распределения вероятности, так что по ней очень легко определить, распределен ли признак нормально или имеет какое-то иное распределение. Обычно выводятся гистограммы сразу для нескольких признаков.
«Ящик с усами» не позволяет увидеть общую картину распределения, зато предоставляет ценную информацию о его параметрах, особенно квантилях. Квантиль – это такое значение признака, что заданный процент значений этого признака в наборе данных меньше этого квантиля. Например, квантиль 50% – это такое значение, что половина значений признака меньше, а вторая половина – больше него, этот квантиль называется медианой. Квантили 0%, 25%, 50%, 75% и 100% называются квартилями, поскольку они делят область определения признака на четыре части.
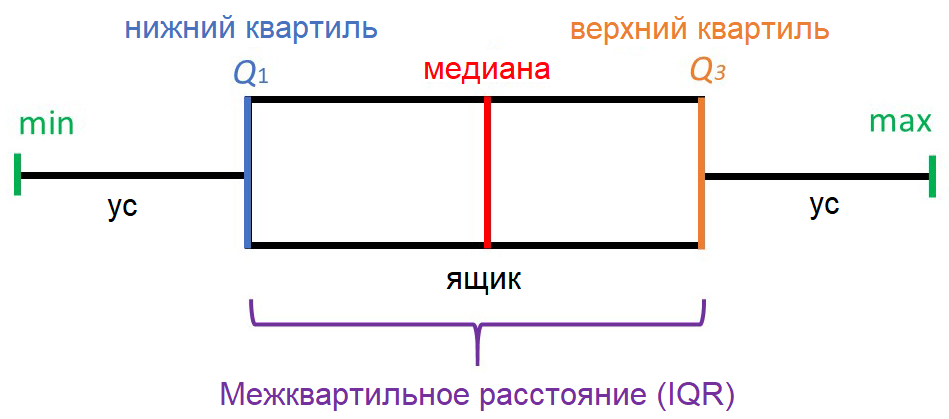
«Усы» выводятся без учета выбросов (outliers) – значений, больших Q3+1.5*IQR или меньших Q1-1.5*IQR. Принято считать, что выбросы скорее свидетельствуют об ошибках ввода данных, чем о реальных значениях признаков, и с ними надо что-то делать – например, удалить. На нашем рисунке выбросы не показаны, а в реальных «ящиках с усами» они выводятся в виде кружков за пределами «усов». Все понятия, о которых мы говорили, изучает статистика.
Анализ зависимостей между признаками
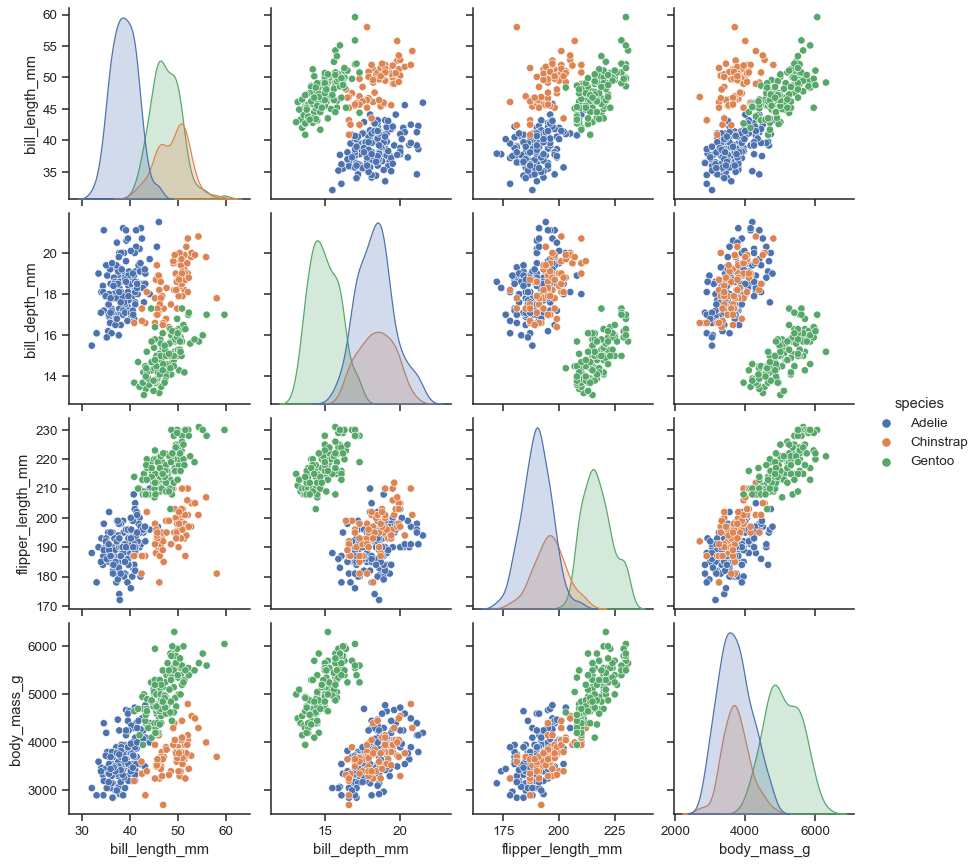
Для исследования возможных зависимостей между признаками используется множество методов, но самые простые из них – попарная диаграмма и матрица корреляции. Начнем с попарной диаграммы (pairplot). Выбираются несколько признаков, зависимости между которыми вы хотите исследовать, и получается комбинированная диаграмма, включающая небольшую диаграмму рассеяния (scatter plot) для каждой пары параметров. В диагональных клетках обычно выводятся графики или гистограммы соответствующих признаков.
Коэффициент корреляции между двумя признаками x и y по набору данных, состоящему из n записей, считается следующим образом («x с крышкой» и «y с крышкой» – средние значения x и y):
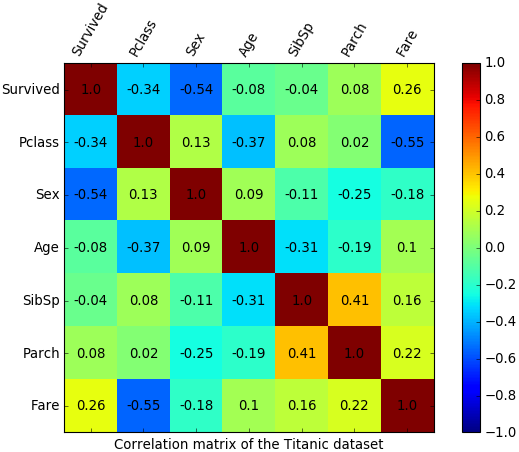
Например, из матрицы корреляции для набора данных о «Титанике» легко увидеть, что какая-то положительная корреляция есть только между количеством родителей и количеством детей на борту: люди плыли либо парами/в одиночку, либо целыми семьями. Отрицательная корреляция есть между пассажирским классом и ценой проезда (естественно, билеты низших по номеру классов стоили дороже) и между полом и признаком выжившего: мужчины уступали места в шлюпках дамам.
Заключение
Как мы уже говорили, статистика занимает особое место в науке о данных, поскольку все данные собираются и обрабатываются именно методами статистики. Более того, иногда вся работа Data Scientist’а, включая создание и усовершенствование моделей, проводится только для того, чтобы доказать или опровергнуть какую-нибудь статистическую гипотезу! А это значит, что каждый Data Scientist обязан знать статистику на профессиональном уровне – по крайней мере, именно такие требования к ним предъявляют на Западе. Помимо статистики придется освоить основы математического анализа и линейной алгебры, о которых шла речь в первых публикациях нашего небольшого цикла.
Если вы хотите наработать необходимую для изучения Data Science математическую базу и подготовиться к углубленным занятиям в «Школе обработки данных» или Computer Science Center, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.